loosening

Recently a classmate gave a talk on proving Nash equilibrium for mixed-strategy games, a proof which used Brouwer's fixed-point theorem.

Brouwer's fixed-point theorem is a theorem rooted in topology: in brief, it states that a continuous deformation of a compact, Informally: bounded, with no missing points. Broadly speaking, compactness generalises finitude. convex set to itself must have at least one fixed point. The apocryphal origin story is that Brouwer once stirred a lump of sugar into his coffee and observed that there was always one stationary point on its dark surface. This armed him with the intuition he then used to state his theorem. But how does it rear its head in game theory?

The core insight is this: you can represent a strategy profile for each player as a simplex Informally: the simplex generalises a triangle. in Euclidean space.

Mixed strategies—strategies that involve random probabilities—are just points in the simplex (the vertices of the simplex are the pure strategies, which are those that involve probabilities of either 0 or 100). Considering the strategy profile for all players involved in the game is just considering multiple simplices simultaneously: what is called a simplotope, which is compact and convex.

The construction of the continuous payoff function mapping the simplotope to itself is a bit more technical, but one can think of it as a way to move continuously inside each simplex, with every little wiggle representing wiggling the payoff of the new strategy profile.

Then one fulfills the hypothesis of Brouwer's theorem, so there must be some fixed point: i.e., a point at which no better payoff can be attained (by change in strategy alone)—otherwise known as a Nash equilibrium.

Often I see proofs that start off as a meticulous, interminable setting-up of things, one providing little to no indication of its longer-term trajectory until the moment before some application of a lemma, a theorem, or a property—all happening in one fell swoop, like a guillotine, almost comically overdetermined, in a way that makes it difficult to imagine how it could've taken any other path. To me the satisfaction of this proof arises from its observation that one can represent something as abstract as strategies in a game, as purely geometric, indeed, topological objects.

It seems like you can get a very lucid insight just from recontextualizing, skillfully and gently manipulating your chosen object of study. Mathematicians are always generalising, which is why some people like to joke that mathematicians make for bad software engineers.

To talk about one of the more interesting instances of this seemingly endless hierarchy of generalisation, I have to return to the simplex, which initially you can take as a point, a line segment, a triangle, then a tetrahedron… In general, a k-simplex is the convex hull Imagine stretching a piece of plastic around points so that all the sides are straight; there is no concavity. of its k+1 vertices, where a point is of course a 0-simplex.

One can define a simplicial complex by gluing simplices together. At this point, though, we're still in geometry land.

Then one can go on to define an abstract simplicial complex (ASC), which suddenly turns the geometric notion of the simplicial complex to a purely combinatorial one. An ASC is a family of finite subsets of a larger set, which is closed under taking subsets. Through the lens of category theory, one can even define a simplicial category and do all kinds of far-flung abstract mathematics. A combinatorial object called a matroid, which generalises linear independence of vectors, is a type of ASC. And since a topology on a point set is, at the end of the day, a subset of the power set of points, we can define an ASC topologically, too.

The surprising thing is that ASCs—despite constituting a much more general concept—align perfectly with the humble 0-simplex, 1-simplex, 2-simplex, In this two-dimensional case, imagine taking any side (face) of a triangle; then the two points comprising the face clearly must be a part of the triangle. and 3-simplex, which feels to me like living in a world where Jörmungandr and garden snakes can coexist without complaint, nor even acknowledgement.

I still recall an anecdote from a senior, who mentioned that as he read Dante's Inferno for a literature class, he stumbled onto a passage where, in hell, the upper portion of a staircase shears and rotates with a groan. The mental image struck him in an entirely unexpected way—it filled in a keystone for a linear algebra proof he had been stuck on for days.

So what am I missing, just from focusing too hard on too little? It's strange, how this diffuse sort of observation can demand as much from us, if not more, as its concentrated form.

There are a lot of motifs in Max Sebald's Austerlitz, but a particularly persistent one is the star-shaped fortress. It takes on many instantiations, including the Theresienstadt Ghetto, which arose out of the fortress town of Terezín, in Czechia. Sebald writes, in the voice of Jacques Austerlitz:

…it had been forgotten that the largest fortifications will naturally attract the largest enemy forces, and that the more you entrench yourself the more you must remain on the defensive, so that in the end you might find yourself in a place fortified in every possible way, watching helplessly while the enemy troops, moving on to their own choice of terrain elsewhere, simply ignored their adversaries’ fortresses…

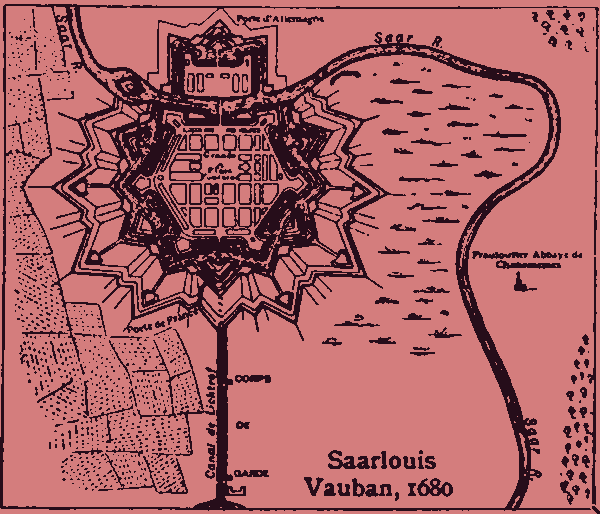
Intention makes for poor currency; revelation occurs precisely when one looks away, or slackens one's grip; receding to the gestalt is a very hard thing to do; it only appears effortless.