infinitude-of-primes
In lieu of a proper farewell to 2024 on this website, this is a showcase of the various ways one can show that there are an infinite number of primes; a simple statement with plenty of surface area to attack.
The explanations are meant to be colloquial and none assume a knowledge of math beyond the first two years of university calculus, except for Dirichlet's proof (4.) which assumes you know the definition of a group, Abelian group, and group homomorphisms (otherwise it would've been even longer than it is now). All but the first proof require quite a bit of set-up and machinery, whereas you could probably fit Euclid's direct proof on a business card if you wanted...
Disclaimer: This page uses Javascript to render \( \KaTeX \).
- Euclid's direct proof
- Euler's proof using the zeta function v1
- Euler's proof using the zeta function v2
- Dirichlet's proof using characters of groups
Direct
Consider a finite list of primes, \( p_1,p_2,\ldots,p_n \). Then consider the product of all of these primes, \( p_1 p_2 \cdots p_n \). Now consider \( P \), the product plus one: \[ P = p_1p_2 \cdots p_n + 1. \] If \( P \) is a prime, we have just found a new prime that was not in our previous list.
If \( P \) is not a prime, then some other prime \( p_i \) divides \( P \). If this \( p_i \) were in our original list, it would also divide \( p_1p_2\cdots p_n \).
But if \( p_i \) divides \( p_1p_2\cdots p_n \) and \( P = p_1p_2\cdots p_n + 1 \), this implies that \( p_i \) divides their difference: \( P - (p_1p_2\cdots p_n) = 1 \). Probably most people would say this is trivial but I say nothing is trivial until you are able to thoroughly convince yourself of it. A scribbly proof: suppose \( p \in \mathbb Z \) divides integers \( a \) and \( b \). By definition this means \( a = pq_1 \) and \( b = pq_2 \) for some \( q_1,q_2 \in \mathbb Z \). This means \( a-b = pq_1 - pq_2 = p(q_1-q_2) \), so \( p \) must divide \( a - b \). \( \blacksquare \) But no prime number divides \( 1 \), so \( p_i \) could not have been in our original list. Thus, in either case, there exists some prime that was not in our original list. \( \blacksquare \)
Since our list was an arbitrary finite list of primes, this shows that for any finite list of primes, there will always exist another prime not contained in the list.
Click for a nice dose of pedantry.
A lot of people have the misconception that this particular proof of Euclid's is a proof by contradiction. In fact, when I was first taught it, I was led to believe that this was an indirect proof.
This is probably because it is often set up with an explicit assumption at the start—suppose that \( p_1,p_2,\cdots,p_n \) are all the primes that exist—and then seeks to contradict this supposition. But we never actually use that supposition anywhere in the proof. This proof applies to any finite list of primes, regardless of if we make the claim that these are all the primes that exist.
Euler v1
Disclaimer: In order to make this a proper
proof, I should have made the definitions of convergence and what it means for a sequence/function to converge, very clear. But since this is an informal exposition, and I don't want to bog the reader down with too much detail so early on, I decided to elide over most of it and to keep explanations more on the side of intuition. This doesn't excuse any possible incorrect statements, so if you see something strange do let me know.
In this section we use the convention that a complex number \( s \in \mathbb C \) can be written \( s = \sigma + it \) where \( \sigma = \Re(s) \), i.e., \( \sigma \) is the real part of \( s \). We don't really do much with the imaginary part, \( \Im(s) = t \), but know that this notation exists and is fairly common (and I love the ridiculously fancy font that TeX uses for it).
Euler's proof uses machinery from analytic number theory, namely the zeta function, which is a function \( \zeta : D \subset \mathbb C \rightarrow \mathbb C\), where \( D = \left\{ s \in \mathbb C \mid s = \sigma + it, \sigma > 1 \right\} \). It is defined by: \[ \zeta(s) \mapsto \sum_{n=1}^{\infty} \frac{1}{n^s} = 1 + \frac{1}{2^s} + \frac{1}{3^s} + \cdots. \] We put such a constraint on our domain (namely, that the real part of \( s \) is strictly greater than \( 1 \)) because the zeta function does not converge otherwise. If you took Calculus II, you might be familiar with the fact that \( \zeta (1) \) is the harmonic series \( \frac{1}{1} + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots \), the classic example of a series whose terms get arbitrarily small (\( \lim_{n\rightarrow\infty} \frac{1}{n} = 0 \)), but actually diverges to infinity.
Zeta function sounds familiar...
You might have heard of the Riemann hypothesis, which is a literal million-dollar problem concerned with the roots of the zeta function's analytic continuation over the complex domain (called the Riemann-Zeta function where we see convergence for input values where \( 0 < \sigma \) and even for \( \sigma < 0 \)).
Though, this is not entirely relevant to what Euler achieved (nearly 100 years before Riemann's functional equation), so I won't go into it further. However if you wish to make one million dollars it may be something you want to investigate personally.
Euler discovered that you could rewrite the zeta function, an infinite sum, as a product over the primes. This is sometimes called the Euler product decomposition: \[ \sum_{n=1}^{\infty} \frac{1}{n^s} = 1 + \frac{1}{2^s} + \frac{1}{3^s} + \cdots = \prod_{p \text{ prime}} \frac{1}{(1-\frac{1}{p^s})}. \] Though this looks pretty implausible, we can gain some intuition as to how in the hell any mere mortal could've made this observation.
First, we introduce the formula for the sum of the geometric series, which is a series of form \[ \sum_{n=0}^\infty r^n = 1 + r + r^2 + r^3 + \cdots. \] This series converges if and only if \( \lvert r \rvert < 1 \), and it has a special formula when this is the case: \[ \sum_{n=0}^\infty r^n = \frac{1}{1-r}. \] Already, we can see the resemblance between \( \frac{1}{1-r} \) in the above formula and \( \frac{1}{1-\frac{1}{p^s}} \) in Euler's product decomposition; let's rewrite it in order to better see this: \[ \frac{1}{1-\frac{1}{p^s}} = \sum_{n=0}^\infty \frac{1}{p^{sn}} = 1 + \frac{1}{p^s} + \frac{1}{p^{2s}} + \frac{1}{p^{3s}} + \cdots \] In other words, every factor of Euler's product decomposition is actually the sum of an infinite geometric series!
Second, we briefly mention the fundamental theorem of arithmetic, which states that any positive integer can be written as the product of prime factors, each raised to a non-negative power—and that this product representation is unique up to ordering. A bit more formally: \[ \forall x \in \mathbb Z^{> 0} ,\quad x = p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_n^{\alpha_n}, \] where \( p_i \) is a prime and \( \alpha_i \in \mathbb N \), and there is only one such factorization for each \( x \). We can then start to envision a relationship between every term of the zeta function's infinite sum \( \frac{1}{x^s} \) (since there is one such term for every positive integer \( x \)), and the reciprocals of the primes in the product decomposition.
Finally, what might seem like a minor observation is actually crucial to why the decomposition works in the first place: the multiplicativity of exponentiation, i.e., \( (xy)^s = x^sy^s \).
So, let's write out the first few terms of the Euler product using what we have just observed, to get a better idea of what it looks like: \[ \prod_{p \text{ prime}} \frac{1}{1-\frac{1}{p^s}} = (1+\frac{1}{2^s}+\frac{1}{2^{2s}}+\cdots)(1+\frac{1}{3^s}+\frac{1}{3^{2s}}+\cdots)(1+\frac{1}{5^s}+\frac{1}{5^{2s}}+\cdots)\cdots \] How would we calculate such a product? Well, in a process analogous to the FOIL method you might have learned in middle school, we choose one term out of each parenthesized infinite sum and multiply them against each other:
Every choice gives us a product that looks like: \[ \frac{1}{2^{e_1 s}} \cdot \frac{1}{3^{e_2 s}} \cdot \frac{1}{5^{e_3 s}} \cdots \] where \( e_i \in \mathbb N \). There are two possibilities for this infinite product: either \( e_i > 0 \) for finitely many \( i \)'s or \( e_i > 0 \) for infinitely many \( i \)'s.
Suppose that \( e_i > 0 \) for finitely many \( i \)'s. Then we ignore all the terms with \( e_i = 0 \) since \( p_i^{0s} = 1 \). So our product looks like \[ \frac{1}{p_1^{e_1 s} p_2^{e_2 s} \cdots p_m^{e_m s}} \] for some finite \( m \). By the multiplicativity of exponentiation, we rewrite this as \[ \frac{1}{(p_1^{e_1} p_2^{e_2} \cdots p_m^{e_m})^s} \]
From the fundamental theorem of arithmetic, it follows that every choice yields a unique fraction \( \frac{1}{n^s} \) where \( n \in \mathbb Z^{>0} \). Then we sum over all such fractions, which is precisely the definition of the zeta function. We have just shown why the Euler product decomposition is reasonable, we haven't even gotten to his actual proof yet! We also don't give a formal proof of the Euler product decomposition here, but here is a link to one if you're interested; it starts pretty much where we left off (with our combinatorial argument based on the fundamental theorem of arithmetic) and involves an interesting sieving
argument. Thankfully, it is pretty concise, and is as follows:
Proof. Suppose there are a finite number of primes \( p_1,p_2,\cdots,p_\ell \). Suppose we have a sequence of real numbers, written \( (\sigma_k)_k \) and \( \lim_{k \rightarrow \infty} \sigma_k = 1 \). According to the Euler product decomposition, we can write: \[ \zeta(\sigma_k) = \prod_{i=1}^\ell \frac{1}{1-\frac{1}{p^{\sigma_k}}}. \] Now we take the limit as \( k \rightarrow \infty \) and thus \( \sigma_k \rightarrow 1 \). The right-hand side converges to \[ \prod_{i=1}^\ell \frac{1}{1-\frac{1}{p}}, \] a finite product. But the left-hand side \( \zeta(\sigma_k) \) diverges.
A further explanation...
...is on its way.One side diverges while another converges? Ridiculous, absurd, contradiction! This means that our original supposition, suppose there are a finite number of primes
, must have been wrong. Thus, there are an infinite number of primes. \( \blacksquare \)
Euler v2
Euler, in his original proof, actually stated a corollary about the growth of primes, and proved a stronger statement:
grow very quickly. (If they did, then this infinite sum would converge.) Compare this with the series \( \sum_{n=0}^\infty \frac{1}{n^2} \), which converges. This gives us the idea that squares grow faster than primes. In order to prove this, we apply the real logarithm to Euler's product decomposition: \[ \begin{align*} \log \zeta(\sigma) &= \log \prod_{p \text{ prime}} \frac{1}{1-\frac{1}{p^\sigma}}\\ &= \sum_p - \log \Big( 1 - \frac{1}{p^\sigma} \Big) \end{align*} \] We rewrite the above expression using the power series expansion of \( \log \) to obtain: \[ \sum_p \sum_{n=1}^\infty \frac{1}{np^{\sigma n}}. \] Then, we split the sum into two pieces: the \( n = 1 \) part and the \( n \ge 2 \) part: \[ \sum_p \frac{1}{p^\sigma} + \sum_p \sum_{n=2}^\infty \frac{1}{np^{\sigma n}}. \] We claim that the second sum converges uniformly. This means that there exists a \( C > 0 \) such that for all \( \sigma > 1 \),
Specifically, Euler also observed that the growth of this series behaves logarithmically, which is related to the fact that for this series to converge, we would want the growth of the denominator to be faster than linear, asymptotically, and logarithmic growth is sublinear, i.e., \( \lim_{n \rightarrow \infty} \frac{x}{\log x} = \infty \).
As someone who has surface level knowledge of asymptotic analysis from computer science classes, Euler's handwaviness here is perfectly fine with me :)
Group theoretic
Background (group of units of \( \mathbb Z/N\mathbb Z \), group characters )
This proof is from Dirichlet and actually repurposes Euler's product decomposition using concepts from group theory. We actually don't need to dive into the expected technicalities of subgroups, congruence classes, conjugates, etc., we can shirk most of the cruft and focus on only what's necessary: the group of units of \( \mathbb Z / N \mathbb Z \), cyclic groups, orders, and characters.
An important ring A ring is a set \( R \) equipped with operations \( + \) and \( \cdot \) which we will call addition
and multiplication
, respectively, such that \( R \) is an abelian group under \( + \) and a monoid under \( \cdot \). (A monoid is like a group, minus the constraint that inverse elements must exist.) Also, multiplication is distributive over addition. A familiar example of a ring is \( (\mathbb Z, +, \cdot) \), i.e., the integers under the usual operations of integer addition and multiplication. we will briefly consider as a starting point is \( \mathbb Z/N\mathbb Z \) (read, Z mod NZ
), whose elements are the integers modulo some other integer \( N \). For example, the elements of \( \mathbb Z/4\mathbb Z \) is the set \( \left\{ \bar 0, \bar 1, \bar 2, \bar 3 \right\} \).
The group of units of \( \mathbb Z/N\mathbb Z\), written \((\mathbb Z/N\mathbb Z)^\times\), is comprised of the invertible elements of \( \mathbb Z/N\mathbb Z \) (the invertible elements in a ring are also called the units). We will also refer to \( (\mathbb Z/N\mathbb Z)^\times \) as \( G_N \) for the sake of notational brevity. The group operation is the familiar integer multiplication, only now we have to consider the modulus, where \( a \cdot b \pmod n \equiv (a \bmod n \cdot b \bmod n) \bmod n \).
Ex: In \( \mathbb Z/4\mathbb Z \), \( \bar 2 \cdot \bar 3 = \bar 2 \), since \[ \begin{align*} 2 \cdot 3 \pmod 4 &= (2 \bmod 4 \cdot 3 \bmod 4) \bmod 4\\ &= 6 \bmod 4\\ &= 2. \end{align*} \] Interestingly, \( \bar 3 \cdot \bar 3 = \bar 1 \). So in \( G_4 \) and in \( G_N \) in general, you can multiply two non-identity elements and get the identity. These are precisely the units. In the case just above, it turns out that \( \bar 3 \) is its own inverse.
But how do we know that any given element in \( \mathbb Z/N\mathbb Z \) is a unit? Using a basic result from number theoryI believe this is Bézout's lemma, which arises from Ěuclidean division., \( (\mathbb Z/N\mathbb Z)^\times \) can be written \( \left\{ n \in \mathbb Z/N \mathbb Z \mid \gcd(n,N) = 1 \right\} \). In other words, \[ n \in \mathbb Z/N\mathbb Z \text{ has a multiplicative inverse } \iff \gcd(n,N) = 1. \] When \( \gcd(n,N) = 1 \) we also say that \( n \) is coprime with \( N \); i.e., they share no common factors other than \( 1 \). We enumerate the elements of some rings of integers modulo \( N \) and their corresponding groups of units below:
\[ \mathbb Z/2\mathbb Z = \left\{ \bar 0, \bar 1 \right\} \] \[ G_2 = (\mathbb Z/2\mathbb Z)^\times = \left\{ \bar 1 \right\} \] \[ \mathbb Z/6\mathbb Z = \left\{ \bar 0, \bar 1, \bar 2, \bar 3, \bar 4, \bar 5 \right\} \] \[ G_6 = (\mathbb Z/6\mathbb Z)^\times = \left\{ \bar 1, \bar 5 \right\} \]
What are the elements of \( \mathbb Z/4\mathbb Z \)? \( G_4\)?
\[
\mathbb Z/4\mathbb Z = \left\{ \bar 0, \bar 1, \bar 2, \bar 3 \right\}
\]
\[
G_4 = \left\{ \bar 1, \bar 3 \right\}
\]
Consider the elements of \( \mathbb Z/2\mathbb Z, \mathbb Z/3\mathbb Z \), and \( \mathbb Z/5\mathbb Z \), and their corresponding group of units \( G_2, G_3 \), and \( G_5 \). Can you make a more general conjecture based off of your observations? Could you prove this conjecture? (Hint: \(2,3,5\) are all prime...)
The observation is that the elements of \( G_p \) for \( p \) prime can be written \( \left\{ \bar 1, \ldots, \overline{p-1} \right\} \). Your explanation should follow something along the lines of the statement that a prime number is coprime to any other number (of course, except for itself).
All \( G_N \)s are examples of finite abelian groups Named after Norwegian mathematician Niels Henrik Abel, who once complained of Gauss's proof style: He is like the fox, who effaces his tracks in the sand with his tail
. which will be of some significance later on.
A cyclic group is a special kind of group, and as you'd expect, describes a group with a cyclic structure. Namely, it is the group you get when you take an element \( g \) and multiply it against itself: \[ \langle g \rangle = \left\{ \ldots, g^{-3}, g^{-2}, g^{-1}, e, g, g^2, g^3, \ldots \right\}. \] In this case, \( g \) is called the generator of the cyclic group and we write \( \langle g \rangle \) to represent the group that \( g \) generates. Despite how it looks, cyclic groups don't necessarily have an infinite number of elements Though infinite cyclic groups do exist, and are isomorphic to the free group (with one generator|of rank 1). An example is the additive group of integers, whose generator is simply \( \left\{ 1 \right\} \). This is a very fancy of way stating that you can get to any integer just by adding to or subtracting \( 1 \) by itself repeatedly.. For example, it's often the case that \( g^k = e \) for some \( k \in \mathbb Z \). Then \( g^{k+1} = g \) and the cycle (lol) continues. More generally it is easy to see that \( g^{nk} = e \) for any \( n \in \mathbb Z \).
The minimal \( k \) such that \( g^k = e \) is called the order of \( g \) and it coincides with the terminology where the order of a group is the number of elements of the group. To see this, let \( g \) be a generator and let the order of \( g \) equal \( 3 \). Then, \[ \langle g \rangle = \left\{ e, g, g^2 \right\} \] since \( g^3 = e \). But where are the inverses, you may ask? Well, note that \( g g^2 = g^2 g = g^3 = e \), so \( g^2 = g^{-1} \). And so on. But in general, the order of an element versus the order of a group is not the same thing.
First we recall the elements of \( G_4 \):
\[
G_4 = \left\{ \bar 1, \bar 3 \right\}.
\]
\( \bar 1 \) clearly has order \( 1 \) since it is the identity. \( \bar 3 \) then cannot have order \( 1 \) by the same reasoning. We check \( (\bar 3)^2 = 3^2 \bmod 4 = \bar 1 \). Thus, \( \bar 3 \) has order \( 2 \) and it is the generator of the cyclic group.Q: \( G_4 \) is a cyclic group with two elements. What are the orders of each element?
The character of a finite Abelian group \( G \) is a group homomorphism \( \chi : G \rightarrow \mathbb C^{\times} \) (where \( \mathbb C^{\times} \) is the multiplicative group of complex numbers sans \( 0 \)).
From this barebones definition it is still possible to conclude some important results: \( \chi(e) = 1 \) and if \( g \) has order \( k \), then \( \chi(g) \) is a \( k \)th root of unity. This should make sense, since if \(g^k = e \), then \( \chi(g^k) = \chi(e) = 1 \), and \( \chi(g^k) = (\chi(g))^k \) by definition of group homomorphism, so \( (\chi(g))^k = 1 \).
What is a root of unity?
An \( n \)th root of unity is a complex number \( z \in \mathbb C \) such that when raised to the \( n \)th power, equals \( 1 \), i.e., \( z^n = 1 \). The set of \( 1 \)st roots of unity is just the singleton set \( \mu_1 = \left\{ 1 \right\} \). The set of \( 2 \)nd roots of unity are \( \mu_2 = \left\{ -1, 1 \right\} \) and the set of \( 4 \)th roots of unity are \( \mu_4 = \left\{ -1,1,i,-i \right\} \).
In general, the \( n \)th roots of unity can be written as \( \mu_n = \left\{ z \in \mathbb C \mid z = \exp(\frac{2k\pi i}{n}) \text{ for } k = 0,\ldots,n-1 \right\} \).
Now we turn to the notion of the group of characters. Suppose we have an abelian group \( G \) and that \( \chi, \chi' \) are two of its characters. Define their product \( \chi\chi' \), another a character, as the following: \[ (\chi\chi')(g) = \chi(g)\chi'(g) \quad \forall g \in G. \] Under this operation we obtain the group of characters of \( G \), or the dual group of \( G \): \[ \widehat{G} = \left\{ \chi : G \rightarrow \mathbb C^\times \mid \chi(gh)=\chi(g)\chi(h) \right\}. \] The identity element of \( \widehat G \) is the trivial/principal character \( \chi_1(g) = 1, \forall g \in G \). To figure out all the other elements of \( \widehat G \) we will need a bit more information.
Say, all the \( G_N \)s we were considering earlier are abelian, and they have a certain structure to them, so let's look into their corresponding dual groups \( \widehat{G}_N \).
We examine \( \widehat{G}_5 \).
One useful relation concerning \( G_N \) and \( \widehat{G}_N \) is the Schur orthogonality relations (there are two of them):
First Schur Orthogonality Relation: For \( \chi \in \widehat{G}_N \), \[ \frac{1}{\lvert G_N \rvert} \sum_{\bar n \in G_N} \chi(\bar n) = \left\{ \begin{array}{l} 1 \quad \chi = \chi_1,\\ 0 \quad \chi \ne \chi_1. \end{array} \right. \]
Second Schur Orthogonality Relation: For \( \bar n \in G_N \), \[ \frac{1}{\lvert G_N \rvert} \sum_{\chi \in \widehat{G}_N} \chi(\bar n) = \left\{ \begin{array}{l} 1 \quad \bar n = \bar 1,\\ 0 \quad \bar n \ne \bar 1. \end{array} \right. \]
The second Schur orthogonality relation states that there exists a linear combination of the \( \chi \)s of \( \widehat{G}_N \) which is nonzero and equal to 1 when its argument is \( \bar 1 \); i.e., it is the (indicator|characteristic) function of \( \left\{ \bar 1 \right\} \subset G_N \).
From this we obtain the linear combination that Dirichlet requires, the indicator function of any \( \bar a \in G_N \).
For \( \bar a \in G_N \), \[ \frac{1}{\lvert G_N \rvert} \sum_{\chi \in \widehat{G}_N} \chi(\bar a^{-1})\chi(\bar a) = \left\{ \begin{array}{l} 1 \quad \bar n = \bar a,\\ 0 \quad \bar n \ne \bar a. \end{array} \right. \]
Dirichlet's theorem on primes in arithmetic progressions
Dirichlet's theorem states that for \( N \ge 2 \), consider \( 0 \le a \le N - 1 \) such that \( \gcd(a,N) = 1 \). Then the sequence \( (a+kN)_{k=0}^\infty \) contains infinitely many primes.
So to consider a concrete example, consider \( N = 8 \) and \( a = 3 \). Certainly, \( 0 \le 3 \le 7\) and \( \gcd(3,8) = 1 \). Then Dirichlet's theorem says that the following sequence
\[
(a+kN)_{k} = (3, 11, 19, 27, 35, \ldots)
\]
contains infinitely many primes. In other words, there are infinitely many primes congruent to \( a \) modulo \( N \) (in this case, \( 2 \bmod 7 \)), which is an even stronger statement than simply saying there are an infinite number of primes
.
In the previous section we went over how Euler proved that
\[
\sum_{p \text{ prime}} \frac{1}{p} = \infty.
\]
Now Dirichlet wants to show that when \( \gcd(a,N) = 1 \),
\[
\sum_{\substack{p \text{ prime},\\ p \equiv a \pmod N}} \frac{1}{p} = \infty.
\]
Showing that the sequence of the reciprocals of your original terms diverges is the same thing as showing that there are an infinite number of them, but additionally that they grow slowly
. Dirichlet's statement builds off of Euler's second proof by saying that even if we only consider a subset of all primes, the sum still diverges.
Dirichlet considers sums of form \[ L(s,\chi) = \sum_{n=1}^\infty \frac{\chi(n)}{n^s} \] now called Dirichlet L-functions. \( \chi \) is a Dirichlet character and \( s \) is a complex number with \( \Re(s) > 1 \). It, too, has an analytic continuation and can be extended to a meromorphic function on the whole complex plane, though we will not be dealing with this extension now.
What makes Dirichlet L-functions useful is that they are completely multiplicative, allowing us to bypass the problem of the product of mods not being multiplicative. Due to their multiplicativity, they can be written as an Euler product in the complex half-plane where \( \sigma > 1 \).
Let us define Dirichlet characters in more detail. They are functions \( \chi : \mathbb N \rightarrow \mathbb C \) satisfying:
- \( \chi(m)\chi(n) = \chi(mn) \) for \( m,n \in \mathbb N\)
- \( \chi(n+N) = \chi(n) \) for \( n \in \mathbb N\)
- \( \chi(n) \ne 0 \) if \( \gcd(n,N) = 1 \) and \( \chi(n) = 0 \) otherwise.
It is fair to be confused on how exactly these \( L \)-functions will get us to the sum desired. But the heart of this proof comes from the fact that due to the Schur orthogonality properties, a linear combination of the \( L \)-functions does equal our desired sum. In other words, \[ c_1(L(s,\chi_1)) + c_2(L(s,\chi_2)) + \cdots + c_n(L(s,\chi_n)) = \sum_{\substack{n=1\\ n \equiv a \mod N}} \frac{1}{n^s}, \] for some \( c_1,c_2\ldots,c_n \in \mathbb C \). We'll write the linear combination as \[ \sum_i c_i L(s,\chi_i) \] for the sake of brevity.
Consider the inequality that lay at the core of Euler's second proof: \[ \log \zeta(\sigma) - C \le \sum_{p \text{ prime}} \frac{1}{p^s} \le \sum_{p \text{ prime}} \frac{1}{p}. \] By showing that the leftmost expression diverged, Euler showed that the rightmost expression also had to diverge, thereby proving the infinitude of primes. We will do something very similar here, by showing that for \( \sigma > 1 \) in this inequality, \[ \sum_i c_i \log L(\sigma,\chi_i) - C \le \sum_{\substack{p \text{ prime}\\p \equiv a \pmod N}} \frac{1}{p^\sigma} \le \sum_{\substack{p \text{ prime}\\p \equiv a \pmod N}} \frac{1}{p}, \] the leftmost expression tends to infinity as \( \sigma \rightarrow 1 \).
Some important differences between Euler's proof and Dirichlet's proof is that for Dirichlet, the leftmost expression is a sum over \( i \). So suppose one \( L \)-function \( L(s,\chi_i) \) has a pole A zero of a complex-differentiable function \( f \) is a point \( z \) such that \( f(z) = 0 \). A pole of a complex-differentiable function \( f \) is a point \( z \) such that \( 1/f(z) = 0 \). A pole is a kind of singularity, which is a point where a function is not well-behaved (i.e., not differentiable or not analytic). at 1 while another \( L \)-function \(L(s,\chi_j) \) has a zero at 1. Then, when we take logarithms, one term in the linear combination goes to \( \infty \) while the other term goes to \( -\infty \) (since \( \log \infty = \infty \) and \( \log 0 = -\infty \)). Adding infinities to negative infinities is unclear, so we will have to carefully consider the behavior of every \( L \)-function near \( s = 1 \) when we take limits.
Let us now define the Dirichlet \( L \)-functions. Consider the group \( G_N \) for some fixed \( N \ge 2 \). Consider the dual group \( \widehat{G}_N \). For a character \( \chi \in \widehat{G}_N \), define \( \tilde\chi : \mathbb N \rightarrow \mathbb C \) via \[ \tilde\chi(n) = \left\{ \begin{array}{l} \chi(\bar n) \quad \text{if } \gcd(n,N) = 1,\\ 0 \quad \text{if } \gcd(n,N) > 1. \end{array} \right. \] Any Dirichlet character \( \tilde \chi \) induces a character \( \chi \in \widehat{G}_N \); just set \( \chi(\bar n) = \tilde \chi(n) \) for \( \bar n \in G_N \). In fact there is a bijection \( \chi \mapsto \tilde\chi \) between \( \widehat{G}_N \) and the set of Dirichlet characters modulo \( N \), so we will simply write \( \chi(n) \) instead of \( \tilde\chi(n) \) to refer to the Dirichlet \( L \)-function; the meaning will be clear from context.
For \( \chi \in \widehat{G}_N \) define the Dirichlet L-function corresponding to \( \chi \) \[ L(s,\chi) = \sum_{n=1}^\infty \frac{\chi(n)}{n^s}. \] The terms of the above sum are only non-zero for \( n \) such that \( \gcd(n,N)=1 \). It is absolutely convergent for \( \Re(s) = \sigma > 1 \), since \( \chi(n) \) can equal either \( 1 \) or \( 0 \), thus \( \lvert \frac{\chi(n)}{n^s} \rvert \le \lvert \frac{1}{n^s} \rvert \) for all \( n \), and so by the comparison test The standard result from Calculus II: if you know \( \sum_n b_n \) converges, and you know that for sufficiently large \( n \), \( 0 \le a_n \le b_n \), then \( \sum_n a_n \) must converge., absolute convergence for \( \sum_n \frac{\chi(n)}{n^s} \) follows from the absolute convergence of \( \zeta(s) = \sum_n \frac{1}{n^s} \).
Here, we'll make a few important claims (I may write down the proof for them later, or at least an explanation) that will be crucial in our final proof of Dirichlet's theorem:
- \( L(s,\chi_1) \) has an analytic continuation to \( \sigma > 0 \) and has a pole at \( s = 1 \) (which arises from the fact that \( \zeta(s) \) has a pole at \( 1 \)).
- For \( \chi \ne \chi_1, L(s,\chi) \) has an analytic continuation to \( \sigma > 0 \) and it does not have a pole at \( s = 1 \) (it turns out with some clever algebra, you can rewrite the partial sum for \( L(\sigma,\chi) \) as an absolutely convergent series for \( \sigma > 0 \)).
- For \( \chi \ne \chi_1, L(1,\chi) \ne 0 \).
Now that we have properly defined Dirichlet \( L \)-functions, we claim that they have an Euler product decomposition: \[ L(s,\chi) = \prod_{p \text{ prime}} \Big( 1-\frac{\chi(p)}{p^s} \Big)^{-1} \] where \( \Re(s) = \sigma > 1 \).
Similarly as before, we don't give a proof of this formula here, but the proof follows the proof for the original product decomposition very closely, using the same sieving argument.
As before, we apply the logarithm to Euler's product decomposition for the \( L \)-functions for each \( \chi \in \widehat{G}_N \):
\[
\log L(s,\chi) = -\sum_p \log \Big( 1-\frac{\chi(p)}{p^s} \Big)
\]
Note we are taking the logarithm of complex numbers. Unlike the real logarithm, the complex logarithm is not an injective function, in fact there are a potentially infinite number of branches each of which differ by a multiple of \( 2\pi \) due to the periodicity of the \( \sin \) and \( \cos \) in Euler's formula (\( e^{\theta i} = \cos(\theta) + i\sin(\theta) \)). In order to force injectivity You might have seen this before in the case of, say, \( \sin \) and \( \arcsin \). Since \( \sin \) is not an injective function (it is \( 2\pi \) periodic), \( \arcsin \) is only defined on the interval \( [-1, 1] \). (which is needed to take the \( \log \), the inverse function of \( \exp \)), we restrict the codomain to a strip
\( (-\pi, \pi] \) which is called the principal branch or the principal logarithm.
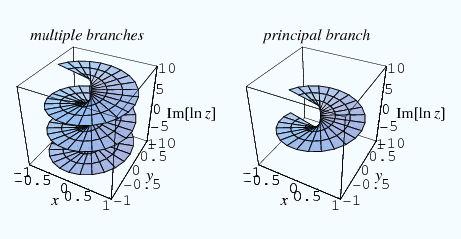
tierof the complex log is exactly \( 2\pi \) apart on the vertical axis.
The principal logarithm has a power series expansion which we use to rewrite the above expression. We will also use the same trick to separate the sum into two parts: one where \( n=1 \) and the other where \( n \ge 2 \):
\[
\log L(s,\chi) = \sum_p\sum_{n=1}^\infty \frac{\chi(p)^n}{np^{sn}} = \sum_p \frac{\chi(p)}{p^{s}} + \sum_p \sum_{n=2}^\infty \frac{\chi(p)^n}{np^{sn}}.
\]
Now, you might be able to guess what we're going to do next, as this part of the proof follows very similarly from Euler's first proof. Indeed, we show the second term in the right-hand side (the double sum where \( n \ge 2 \)) to be convergent by taking its norm:
\[
\Big\lvert \sum_p\sum_{n=2}^\infty \frac{\chi(p)^n}{np^{sn}} \Big\rvert \le \sum_p\sum_{n=2}^\infty \frac{\chi(p)^n}{np^{\sigma n}} \le 1 \quad \text{ for } \sigma > 1
\]
We know that the norm of the second term is then bound by some constant \( C > 0 \). We write this using Big-O
notation:
how does varying input size effect my program's runtime.
We're basically done. Since \[ \sum_{p \equiv a} \frac{1}{p^\sigma} \le \sum_{p \equiv a} \frac{1}{p}, \] and the left-hand side must diverge as \( \sigma \rightarrow 1 \), the right-hand side must diverge, and this is exactly what we wanted to show.
Now, the big corollary to all of this work, the cherry on top of the towering sundae, is that there are an infinite number of primes congruent to an \( a \) modulo \( N \), which implies that there are an infinite number of primes in general. \( \blacksquare \)
I know this proof sort of has the vibe of using a industrial-grade tractor to build a small sandcastle. But it turns out that in order to prove Dirichlet's theorem in its full generality, we needed some pretty powerful tools from analytic number theory and group theory. Some proofs also use calculus.